LOS ÁNGULOS
Las aplicaciones de los angulos en la vida cotidiana:
* En la construccion de casas, escaleras, etc.
* En las direcciones a seguir de los barcos, aviones y otros
* Los angulos se utilizan mas frecuentemente para calcular las fuerzas sobre un objeto, como cuando se hace diagrama de cuerpo libre o quieres encontrar la fuerza apropiada para un sistema de poleas o un estructura que requiera de cierto tipo de angulo.
Definición y características
- Forma geométrica: Se denomina "ángulo" a la amplitud entre dos líneas de cualquier tipo que concurren en un punto común llamado vértice. Coloquialmente, ángulo es la figura formada por dos líneas con origen común. El ángulo entre dos curvas es el ángulo que forman sus rectas tangentes en el punto de intersección.
- Forma trigonométrica: Es la amplitud de rotación o giro que describe un segmento rectilíneo en torno de uno de sus extremos tomado como vértice desde una posición inicial hasta una p
- osición final. Si la rotación es en sentido levógiro (contrario a las manecillas del reloj), el ángulo se considera positivo. Si la rotación es en sentido dextrógiro (conforme a las manecillas del reloj), el ángulo se considera negativo.
- Radián (usado oficialmente en el Sistema Internacional de Unidades)
- Grado centesimal
- Grado sexagesimal
Clasificación de ángulos
| Tipo | Descripción |
|---|---|
| Ángulo nulo | Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de 0°. |
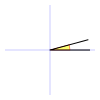
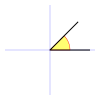
Ángulo agudo  | Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de 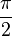 rad. Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales). rad. Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales). |
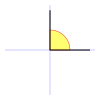
Ángulo recto 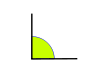 | Un ángulo recto es de amplitud igual a 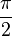 rad Es equivalente a 90° sexagesimales (o 100g centesimales). rad Es equivalente a 90° sexagesimales (o 100g centesimales).Los dos lados de un ángulo recto son perpendiculares entre sí. La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice. |
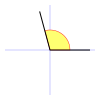
Ángulo obtuso  | Un ángulo obtuso es aquel cuya amplitud es mayor a 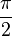 rad y menor a rad y menor a 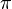 rad Mayor a 90° y menor a 180° sexagesimales (o más de 100g y menos de 200g centesimales). rad Mayor a 90° y menor a 180° sexagesimales (o más de 100g y menos de 200g centesimales). |
Ángulo llano, extendido o colineal  | El ángulo llano tiene una amplitud de 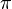 rad Equivalente a 180° sexagesimales (o 200g centesimales). rad Equivalente a 180° sexagesimales (o 200g centesimales). |
Ángulo oblicuo  | Ángulo que no es recto ni múltiplo de un ángulo recto. Los ángulos agudos y obtusos son ángulos oblicuos. |
| Ángulo completo o perigonal  | Un ángulo completo o perigonal, tiene una amplitud de  rad Equivalente a 360° sexagesimales (o 400g centesimales). rad Equivalente a 360° sexagesimales (o 400g centesimales). |
Ángulos convexo y cóncavo
En un plano, dos semirrectas (no coincidentes ni alineadas) con un origen común determinan siempre dos ángulos, uno convexo (el de menor amplitud) y otro cóncavo (el de mayor amplitud):| Tipo | Descripción |
|---|---|
| Ángulo convexo o saliente  | Es el que mide menos de 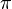 rad. Equivale a más de 0° y menos de 180°sexagesimales (o más de 0g y menos de 200g centesimales). rad. Equivale a más de 0° y menos de 180°sexagesimales (o más de 0g y menos de 200g centesimales). |
| Ángulo cóncavo, reflejo o entrante  | Es el que mide más de 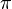 rad y menos de rad y menos de  rad. Esto es, más de 180° y menos de 360° sexagesimales (o más de 200g y menos de 400g centesimales). rad. Esto es, más de 180° y menos de 360° sexagesimales (o más de 200g y menos de 400g centesimales). |
Ángulos relacionados
En función de su posición, se denominan:- ángulos adyacentes, los que tienen un vértice y un lado común, pero no tienen ningún punto interior común,
- ángulos consecutivos, los que tienen un lado y el vértice común,
- ángulos opuestos por el vértice, aquellos cuyos lados son semirrectas opuestas.
- ángulos correspondientes, formados por dos paralelas y una transversal.
- ángulos congruentes, aquellos que tienen la misma amplitud, es decir, que miden lo mismo,
- ángulos complementarios, aquellos cuya suma de medidas es π/2 radianes o 90°,
- ángulos suplementarios, aquellos cuya suma de medidas es π radianes o 180°,
- ángulos conjugados, aquellos cuyas medidas suman 2π radianes o 360°.
Ángulos de un polígono
En función de su posición, se denominan:- ángulo interior o interno de un polígono, es el formado por lados adyacentes, interiormente.
- ángulo exterior o externo de un polígono, es el conformado por un lado y la prolongación del adyacente.
- Ángulo central, si tiene su vértice en el centro de ésta.
- La amplitud de un ángulo central es igual a la del arco que abarca.
- La amplitud de un ángulo inscrito es la mitad de la del arco que abarca.
- La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
- La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones;
- La amplitud de un ángulo, no es la mitad de la diferencia de los dos arcos que abarcan sus lados sobre dicha circunferencia.
Ángulos respecto de una circunferencia
Galería de ángulos
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 | |||||
 |



Brayan, lo que se quiere del trabajo es la aplicación en la vida diaria de un tema (no la clase)y finalmente poner las conclusiones de lo que entiendes.OK?
ResponderEliminarBueno de verdad no hay mucho que comentar porque solo has puesto 3 aplicaciones y mas toda la clase de angulos, bueno sobre tus aplicaciones si se da en la contruccion de casas, edificios, escaleras, etc, porque los ingenieros y arquitectos hacen los planos con los angulos correspondientes para que no halla errores a la hora de contruir y esto no provoque desnivelaciones o desequilibrio en las construccione. En los que las direcciones de los barcos y aviones no me queda muy claro, sino me equivovo creo que cada uno tiene como un radar o se guian por mapas a donde quieren ir, claro que no estoy seguro, seria bueno que lo expliques mejor porque no se entiende esa parte. En la ultima se se usa para hallar fuerzas lo que ya vendria a ser fisica para hallar cuanto se desplazo un cuerpo con una fuerza.
ResponderEliminarno
ResponderEliminar